Bài 1 trang 17 sgk giải tích 11
Bài 1. Hãy xác định các giá trị của trên đoạn
để hàm số
| a) Nhận giá trị bằng 0 ; | b) Nhận giá trị bằng 1 ; |
| c) Nhận giá trị dương ; | d) Nhận giá trị âm. |
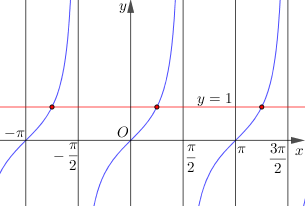
a) Trục hoành cắt đoạn đồ thị (ứng với
) tại ba điểm có hoành độ
Do đó trên đoạn chỉ có ba giá trị của
để hàm số
nhận giá trị bằng 0, đó là
b) Đường thẳng cắt đoạn đồ thị
(ứng với
) tại ba điểm có hoành độ
. Do đó trên đoạn
chỉ có ba giá trị của
để hàm số
nhận giá trị bằng 1, đó là
;
;
c) Phần phía trên trục hoành của đoạn đồ thị
(ứng với
) gồm các điểm của đồ thị có hoành độ truộc một trong các khoảng
;
Vậy trên đoạn , các giá trị của
để hàm số
nhận giá trị dương là
d) Phần phía dưới trục hoành của đoạn đồ thị
(ứng với
) gồm các điểm của đồ thị có hoành độ thuộc một trong các khoảng
,
Vậy trên đoạn , các giá trị của x để hàm số
nhận giá trị âm là
,
Được tài trợ