Bài 3 trang 18 SGK Hình học 12
Chứng minh rằng tâm của các mặt của hình tứ diện đều là các đỉnh của một hình tứ diện đều.
+) Xét tứ diện đều có cạnh bằng
Gọi
lần lượt là trọng tâm các tam giác
và
lần lượt là trung điểm của
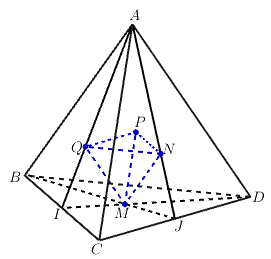
+) Theo tính chất trọng tâm tam giác ta có : đồng dạng với
. Do đó
+) Tương tự
+) Dựng hình và chứng minh tương tự ta có :
+) Vậy ta có là tứ diện đều.
Được tài trợ