Bài 4 trang 18 SGK Hình học 12
|
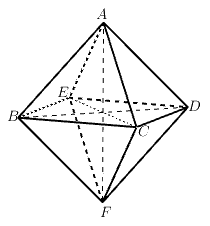
Cho hình bát diện đều Chứng minh rằng : a) Các đoạn thẳng b) |
Hình 1.24 |
(h.1.24).
và 
đôi một vuông góc với nhau và cắt nhau tại trung điểm mỗi đường.
và 
là những hình vuông.
a)
+) Vì 
cách đều 
và 
nên chúng đồng phẳng. Tương tự ta có 
đồng phẳng, 
đồng phẳng.
+) Trong mặt phẳng 
gọi 
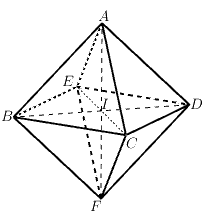
+) Mặt khác 
+) Vậy 
đồng quy tại 
+) 
là các hình thoi nên 
và 
là trung điểm của 
b)
+) Ta có 
là các hình thoi.
+) Mặt khác 
là hình vuông.
+) Tương tự ta có cũng là hình vuông.
Được tài trợ