I-Nhắc lại lý thuyết

1) Định nghĩa sự đồng biến, nghịch biến của hàm số.

Cho hàm số  xác định trên khoảng , với mọi . Khi đó : 

•  đồng biến trên  khi và chỉ khi .
•  nghịch biến trên  khi và chỉ khi .

2) Mối quan hệ giữa tính đơn điệu(đồng biến,nghịch biến) của hàm số và dấu của đạo hàm.

• Nếu  thì  đồng biến trên .
• Nếu thì  nghịch biến trên .

II-Tìm m để hàm số đồng biến, nghịch biến trên khoảng K là 

  * Phương pháp giải :  

• Bước 1. Tính .  Hàm số đồng biến(nghịch biến) trên  thì .
• Bước 2. Thường gặp y' là một tam thức bậc hai nên ta dựa vào các nhận xét sau để tìm  :

                       + Bất phương trình 

                       + Bất phương trình 

   * Ví dụ minh họa : 

Ví dụ 1 : Tìm  để hàm số  đồng biến trên .

A.

B.

C.

D.

Lời giải : 

• Ta có 
• Hàm số đồng biến trên  khi :

• Chọn D.

Ví dụ 2: Tìm  để hàm số  nghịch biến trên 

A..

B..

C..

D..

Lời giải : 

• Ta có 
• Hàm số đồng biến trên  khi 

     Chọn B.

Ví dụ 3 : Với những giá trị nào của  thì hàm số  luôn đồng biến trên tập số thực.

A.

B.

C.

D.

Lời giải : 

           Ta có . Vì hệ số  của  còn phụ thuộc  nên ta xét hai trường hợp sau : 

• Trường hợp 1 : Với  ta có  nên hàm số nghịch biến trên  (vì ) và đồng biến trên  Do đó  không thỏa mãn yêu cầu bài toán.
• Trường hợp 2 : Với , để hàm số đồng biến trên tập số thực  khi 
• Chọn C.

III-Tìm m để hàm số đồng biến, nghịch biến trên khoảng K là tập con của 

1)  Phương pháp "Cô lập tham số m" :

* Phương pháp giải :      

Cho hàm số  có đạo hàm trên K.

• Bước 1. Tính . Hàm số đồng biến(nghịch biến) trên K thì  .
• Bước 2.  Đưa bất phương trình  về dạng  hoặc  (ta gọi đây là bước cô lập m)
• Bước 3. Tìm  dựa vào hai nhận xét sau :

* Ví dụ minh họa.

Ví dụ 1 : Tìm tất cả các giá trị của tham số  để hàm số  đồng biến trên 

A. .

B.

C..

D..

Lời giải : 

• .
• Hàm số đồng biến trên khoảng  khi

         .

• Nhận xét rằng , do đó : 

• Chọn B.

Ví dụ 2 : Tìm tất cả các giá trị của tham số  để hàm số  nghịch biến trên 

A..

B.

C..

D..

Lời giải : 

• .
• Để hàm số nghịch biến trên khoảng  ta có 
• Xét  hay hàm số đồng biến trên , do đó : 
• Chọn C.

Ví dụ 3 : Tìm tất cả các giá trị của tham số  để hàm số  đồng biến trên khoảng 

A..

B.

C.

D.

Lời giải : 

• Ta có .
• Hàm số đồng biến trên  khi 
•  với 
•  Ta có  .
• Bảng biến thiên của  

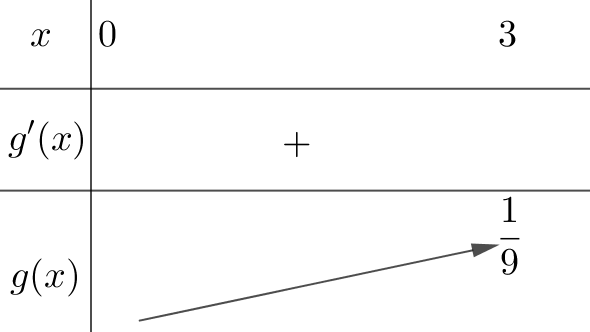
• Từ bảng biến thiên ta có  Chọn A.

Ví dụ 4 : Tìm tất cả các giá trị của tham số  để hàm số  đồng biến trên khoảng 

A.

B.

C.

D.

Lời giải : 

• Ta có .
• Hàm số đồng biến trên  khi 
• Chọn B.

2) Phương pháp sử dụng bảng biến thiên giải dạng toán tìm m để hàm số đồng biến (nghịch biến) trên một khoảng: 

    Đây là phương pháp tương đối dài dòng và phức tạp nhưng lại giải quyết được hầu hết các trường hợp, đặc biệt là những bài toán mà chúng ta không thể cô lập được tham số m.

* Phương pháp giải : 

• Bước 1. Tính  Hàm số đồng biến(nghịch biến) trên K thì  
• Bước 2. Lập bảng biến thiên của hàm số dựa vào dấu 
• Bước 3. Từ bảng biến thiên và đề bài kết luận giá trị của 

* Chú ý :

• Nếu dấu của đạo hàm phụ thuộc vào dấu của một tam thức bậc hai thì ta phải xét hai trường hợp  và 
• Khi sử dụng phương pháp này ta thường dẫn đến việc so sánh các nghiệm của một tam thức bậc hai với một số  liên quan. Khi đó ta có thể đưa bài toán đến việc vận dụng định lý Vi-et bằng cách sử dụng các kết quả sau : 

2.  .

* Ví dụ minh họa.

Ví dụ 1 : Tìm m để hàm số  nghịch biến trên 

A.

B.

C.

D.

Lời giải : 

Ta có 

Để hàm số nghịch biến trên ta có .

*Trường hợp 1 :

• Nếu  thì  (tam thức bậc hai có  thì cùng dấu với hệ số ). 
• Vậy không thỏa mãn yêu cầu bài toán.

*Trường hợp 2 :

• Nếu  thì  có hai nghiệm phân biệt .Ta có bảng biến thiên như sau

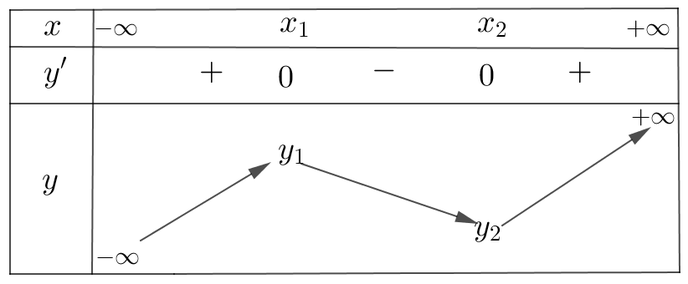
• Dựa vào bảng biến thiên để hàm số nghich biến trên ta phải có .
• Chọn C

Ví dụ 2 : Tìm để hàm số đồng biến trên 

A.

B.

C.

D.

Lời giải : 

Ta có

Hàm số đồng biến trên  khi .

*Trường hợp 1 :

• Nếu   thì . Do đó hàm số đồng biến trên  nên cũng đồng biến trên  
• Vậy thỏa yêu cầu bài toán (1)  

*Trường hợp 2 :

• Nếu  thì có hai nghiệm phân biệt Ta có bảng biến thiên như sau

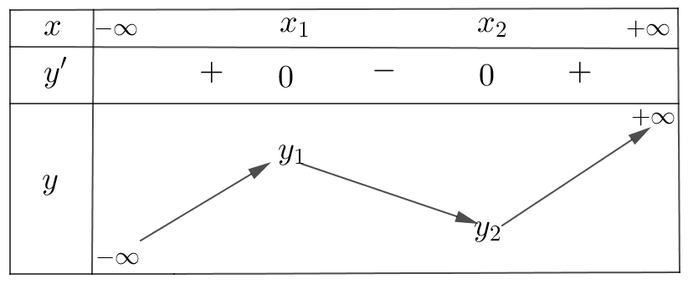
• Dựa vào bảng biến thiên để hàm số đồng biến trên  thì , có nghĩa là  có hai nghiệm thỏa 
• Kết hợp với điều kiện ta có    (2)

Từ (1) và (2) ta có  Chọn A.

Lời bình : Đây là các ví dụ mà chúng ta không thể cô lập được m, vì vậy buộc ta phải dựa vào "bảng biến thiên" để giải quyết. Như vậy khi giải quyết bài toán dạng này cần linh hoạt sử dụng các phương pháp trên vì mỗi phương pháp đều có điểm mạnh và điểm yếu của nó.