I. Diện tích mặt cầu:

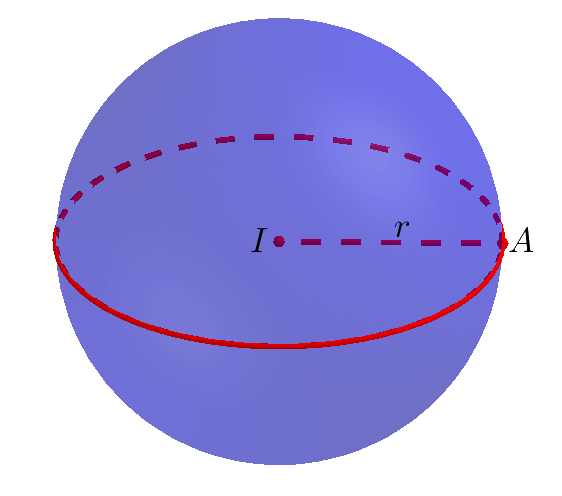
Diện tích mặt cầu có bán kính   là 

II. Thể tích khối cầu : 

Thể tích khối cầu có bán kính   là 

Chú ý : Để tính diện tích mặt cầu hay thể tích khối cầu ta chỉ cần tìm bán kính của mặt cầu đó.

III. Phương trình mặt cầu :

Trong không gian với hệ trục , phương trình mặt cấu có hai dạng như sau : 

• Dạng 01 :  là mặt cầu có tâm   và bán kính .
• Dạng 02 :  với  là mặt cầu có tâm  và bán kính  

IV. Một số ví dụ liên quan đến diện tích mặt cầu và thể tích khối cầu.

Ví dụ 1. Tính diện tích mặt cầu và thể tích khối cầu có đường kính bằng 

Lời giải : 

Mặt cầu có đường kính bằng  nên có bán kính  Khi đó : 

• Diện tích mặt cầu : 
• Thể tích khối cầu : 

Ví dụ 2. Trong hệ trục tọa độ  cho mặt cầu có phương trình . Tính diện tích mặt cầu và thể tích khối cầu có phương trình như trên.

Lời giải : 

Mặt cầu có bán kính   Khi đó : 

• Diện tích mặt cầu : 
• Thể tích khối cầu : 

Ví dụ 3. Trong hệ trục tọa độ  cho mặt cầu có phương trình . Tính diện tích mặt cầu và thể tích khối cầu đó.

Lời giải : 

Ta có  nên mặ cầu có  Khi đó : 

• Diện tích mặt cầu : 
• Thể tích khối cầu : 

Ví dụ 4. Trong hệ trục tọa độ , tính diện tích mặt cầu và thể tích khối cầu có tâm  và tiếp xúc với mặt phẳng 

Lời giải : 

Vì mặt cầu tiếp xúc với mặt phẳng  nên bán kính mặt cầu bằng khoảng cách từ tâm  tới mặt phẳng  hay  Khi đó : 

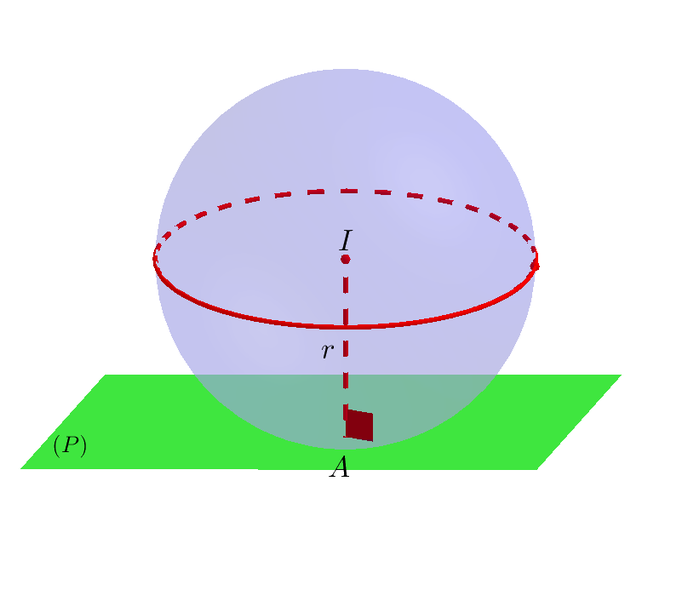
• Diện tích mặt cầu : 
• Thể tích khối cầu : 

Ví dụ 5. Trong hệ trục tọa độ , một mặt phẳng  cắt mặt cầu  có tâm  theo một đường tròn có bán kính  Tính thể tích khối cầu 

Lời giải : 

Gọi  là tâm đường tròn giao tuyến (tức là hình chiếu của   xuống ). Khi đó tam giác  vuông tại  nên  hay .

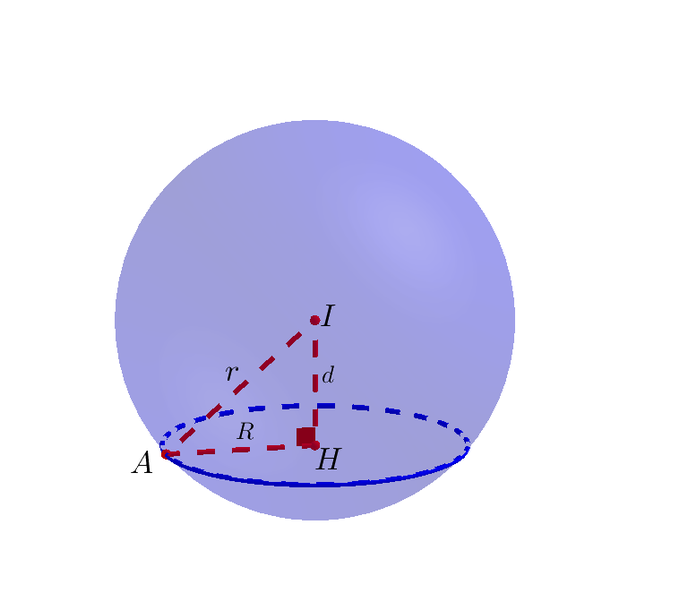
Mặt khác : 

Vậy thể tích khối cầu là