Bài 3 trang 121 SGK Hình học 11
Hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh SA = a và vuông góc với mặt phẳng (ABCD).
a) Chứng minh rằng các mặt bên của hình chóp là những tam giác vuông.
b) Mặt phẳng (α) đi qua A và vuông góc với cạnh SC lần lượt cắt SB, AC, SD tại B', C', D'. Chứng minh B'D' song song với BD và AB' vuông góc với SB.
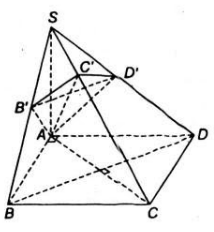
a) SA⊥(ABCD)⇒SA⊥AB; SA⊥AD⇒ΔSAB,ΔSAD là các tam giác vuông tại A.
Ta có: vuông tại B.
Tương tự: vuông tại D.
b) Ta có BC⊥(SAB)(cmt)⇒AB′⊥BC.
Mà AB′⊂(α)⇒AB′⊥SC⇒AB′⊥(SBC)⇒AB′⊥SB.
Chứng minh tương tự ta có AD′⊥(SCD)⇒AD′⊥SD.
Ta chứng minh được ΔSAB=ΔSAD(c.g.c)⇒AB'=AD′ (hai đường cao xuất phát từ 2 đỉnh tương ứng).
Do đó A thuộc trung trực của B′D′ (1).
Ta cũng có: SB′=SD′;
ΔBSC=ΔDSC⇒
Do đó ΔB′SC′=ΔD′SC′(c.g.c)⇒C′D′=C′B′.
Do đó C′ thuộc trung trực của B′D′.
Từ (1) và (2) suy ra AC′AC′ là đường trung trực của D′B′ do đó D′B′⊥AC′ (3)
Mặt khác: SC⊥(α); D′B′⊂(α) ⇒SC⊥D′B′ (4)
Từ (3) và (4) suy ra: D′B′⊥(SAC) (5)
Ta có:
Từ (5) và (6) ⇒D′B′//DB.