Bài 3 trang 121 SGK Giải tích 12

+) Đường tròn có tâm là gốc tọa độ, bán kính  có phương trình:

+) Tọa độ giao điểm của Parabol và đường tròn  là nghiệm của hệ:

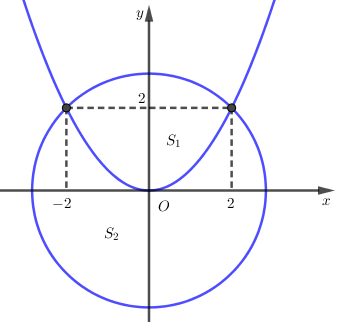
+) Khi đó diện tích hình phẳng  giới hạn bởi parabol và đường tròn là:

+) Tính 

• Đặt 

Đổi cận :

•   ta có 
•    ta có 
• Vậy 

+) Vậy 

+) Mặt khác diện tích hình tròn là: