Bài 5 trang 121 SGK Giải tích 12
Cho tam giác vuông có cạnh
nằm trên trục
. Đặt
Gọi
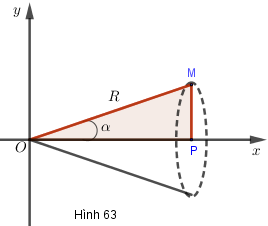
là khối tròn xoay thu được khi quay tam giác đó xung quanh trục
(H.63).
a) Tính thể tích của theo
và
b) Tìm sao cho thể tích của
lớn nhất.
a) Tính thể tích của :
+) là khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi đường thẳng
+) Đường thẳng đi qua
và tạo với trục hoành một góc
(hệ số góc
) nên có phương trình:
.
+) Mặt khác
+) Khi đó thể tích của là :
b) Tìm để
lớn nhất :
+) Đặt nên
. Xét hàm số
+) Do đó :
+) Vậy lớn nhất khi
hay
Được tài trợ