Bài 6 trang 26 SGK Hình học 12

+) Giả sử hai đoạn thẳng  có vị trí như hình vẽ với  là đoạn vuông góc chung của  và .          

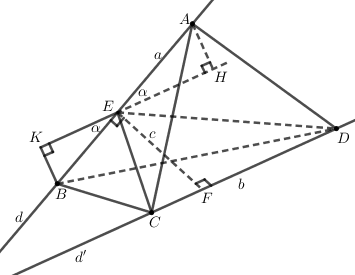
+) Trong  kẻ đường thẳng qua  song song với . Gọi  lần lượt là hình chiếu của  lên đường thẳng này, gọi  là góc giữa  và . Khi đó 

+) Ta có  và 

+) Tương tự ta cũng có 

+) 

+) Vậy thể tích tứ diện  không đổi.