Bài 5 trang 26 SGK Hình học 12
Cho tam giác 
vuông cân ở 
và 
. Trên đường thẳng qua 
và vuông góc với mặt phẳng 
lấy điểm 
sao cho 
Mặt phẳng qua vuông góc với 
, cắt tại 
và cắt 
tại 
. Tính thể tích khối tứ diện 
theo 
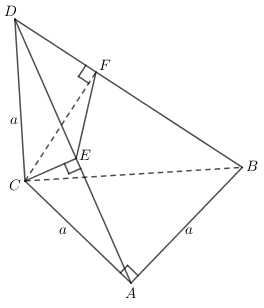
+) Theo giả thiết ta có 
+) 
+) Từ 
ta có 
+) Ta có : 
![]()
![]()
vuông cân tại ![]()
![]()
vuông tại ![]()
là đường cao nên ![]()
vuông cân tại 
vuông tại 
là đường cao nên 
+) Vậy 
Được tài trợ