Bài 4 trang 25 SGK Hình học 12
Cho hình chóp 
. Trên các đoạn 
lần lượt lấy ba điểm 
khác với 
. Chứng minh rằng 
+) Gọi 
lần lượt là hình chiếu của 
lên mặt phẳng 
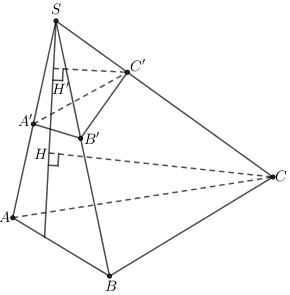
+) Khi đó : 
+) Mặt khác :
-
![]()
đồng dạng với ![]()
nên ![]()
![]()
đồng dạng với 
nên 
+) Vậy 
Được tài trợ