Câu 7 Trang 99 SGK Hình học 10
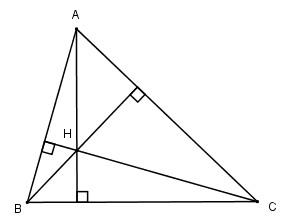
Bài 7. Cho tam giác ABC với H là trực tâm. Biết phương trình của đường thẳng AB,BH và AH lần lượt là: 4x+y–12=0, 5x–4y–15=0 và 2x+2y–9=0
Hãy viết phương trình hai đường thẳng chứa hai cạnh còn lại và đường cao thứ ba.
Tọa độ đỉnh A là nghiệm của hệ:
Đường thẳng BH:5x–4y–15=0 có vecto chỉ phương
Cạnh AC vuông góc với BH nên nhận vecto u làm một vecto pháp tuyến, AC đi qua A(52,2) và có vecto pháp tuyến nên có phương trình là:
Tương tự, tọa độ đỉnh B là nghiệm của hệ:
AH:2x+2y–9=0 có vecto chỉ phương
BC vuông góc với AH nên nhận vecto làm vecto pháp tuyến, phương trình BC là:
−1(x−3)+(y−0)=0⇔x−y−3=0
Tọa độ H là nghiệm của hệ phương trình:
Đường cao CH đi qua H và vuông góc với AB
Hoàn toàn tương tự, ta viết được phương trình của CH:
CH:3x–12y–1=0.
Được tài trợ