Bài 1 trang 18 SGK Giải tích 12
Áp dụng Quy tắc I, hãy tìm các điểm cực trị của các hàm số sau:
| a) |
b) |
| c) |
d) |
| e) |
a)
- Tập xác định:
- Bảng biến thiện:
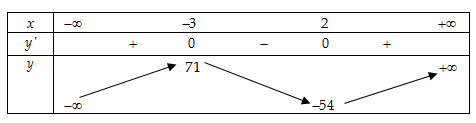
- Dựa vào bảng biến thiên hàm số có điểm cực đại là
và điểm cực tiểu là
.
b)
- Tập xác định:
(vì
)
- Bảng biến thiên:
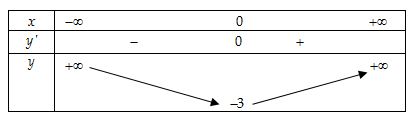
- Vậy hàm số có một điểm cực tiểu là
.
c)
- Tập xác định:
- Bảng biến thiên:
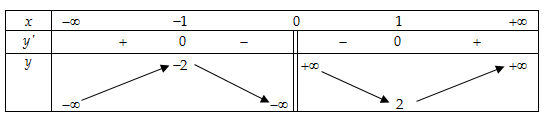
- Vậy điểm cực đại là
,điểm cực tiểu là
.
d)
- Tập xác định:
- Bảng biến thiên:
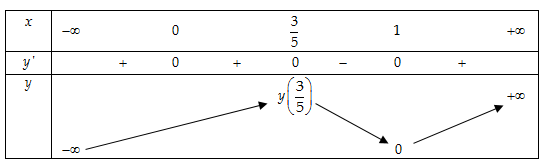
- Vậy hàm số đạt cực đại tại
, đạt cực tiểu tại
.
e)
- Tập xác định:
(vì
).
- Bảng biến thiên:
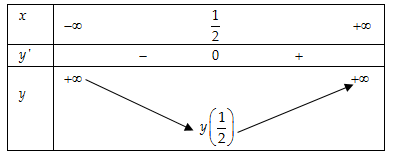
- Vậy hàm số đạt cực tiểu tại
Được tài trợ