Bài 2 trang 29 SGK Hình học 11

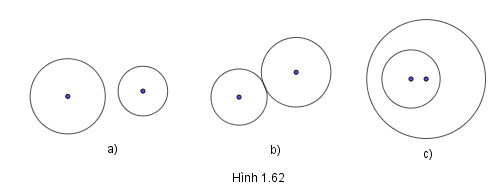
Hình a)

Gọi 

Kẻ đường kính từ đó dựng bán kính của đường tròn sao cho bán kính   song song với  Nối   giao với 

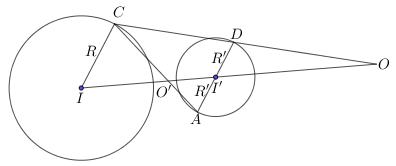
Khi đó :

+  đồng dạng  nên :

+ Tương tự :  đồng dạng  nên 

Vậy có hai tâm vị tự tương ứng với các tỉ số vị tự là 

Hình b)

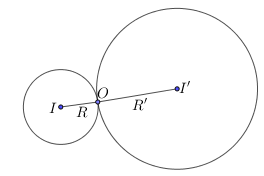
Gọi  là điểm tiếp xúc của hai đường tròn. Ta có : 

Vậy tâm vị tự là ,  tỉ số vị tự là 

Hình c)

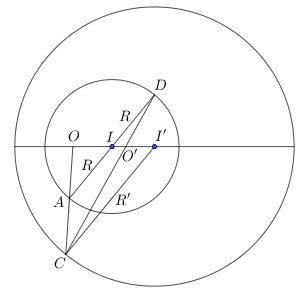
Tương tự : Dựng đường kính  của đường tròn tâm , vẽ bán kính  Khi đó bằng cách xét các cặp tam giác đồng dạng  ta tìm được hai tâm vị tự là , tỉ số vị tự lần lượt là  (ta xét như  là ảnh của )