Bài 5 trang 119 SGK Hình học 11

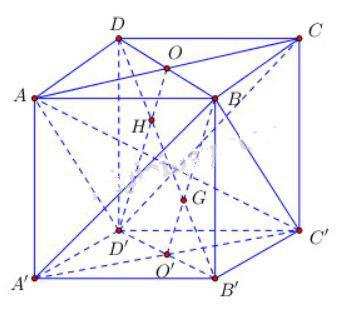
a) Ta có B′A′=B′B=B′C′

⇒B′ thuộc trục của tam giác A′BC′          (1)

DA′=DB=DC′(đường chéo các hình vuông bằng nhau)

⇒D cũng thuộc trục của tam giác A′BC′    (2)

Từ (1) và (2) ⇒B′D là trục của (BA′C′) ⇒⊥(BA′C′). 

b) Chứng minh tương tự ta được B′D⊥(ACD′)

Gọi

Ta có:

O′G//D′H, O′ là trung điểm của B′D′⇒G là trung điểm của B′H.

⇒  (3)

OH//GB, O là trung điểm của BD⇒H là trung điểm của DG.

⇒HG=HD  (4)

Từ (3) và (4) suy ra: GB′=GH=HD⇒GH=B′D

Do ABCD.A′B′C′D′ là hình lập phương cạnh a

⇒B′D=

⇒HG=.

Vậy d((BA′C′);(ACD′))=.

c) 

Vậy .