Bài 3 trang 119 SGK Hình học 11
Bài 3 (trang 119 SGK Hình học 11): Cho hình lập phương ABCD.A'B'C'D' cạnh a. Chứng minh rằng các khoảng cách từ các điểm B, C, D, A', B' và D' đến đường chéo AC' đều bằng nhau. Tính khoảng cách đó.
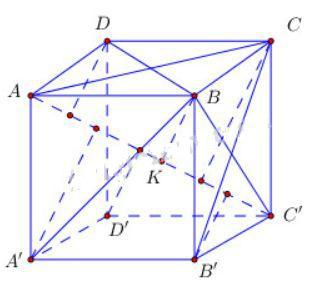
Gọi K là hình chiếu của B trên AC′.
Ta có AB⊥(BCC′B′)⇒AB⊥BC′⇒ΔABC′ vuông tại B.
Dễ thấy BC′ là đường chéo của hình vuông cạnh a⇒BC′=.
Áp dụng hệ thức lượng trong tam giác vuông ABC′ có:
Ta có:
ΔABC′=ΔC′CA=ΔADC′=ΔAA′C′=ΔC′B′A=ΔC′D′A (c.g.c)
Do đó các chiều cao tương ứng của các tam giác bày bằng nhau, chứng tỏ khoảng cách từ B,C,D,A′,B′,D′ tới AC′ đều bằng .
Được tài trợ