Bài 3 trang 99 SGK Hình học 12
Cho mặt cầu tâm
bán kính
. Hình nón có đường tròn đáy
và đỉnh
đều thuộc
được gọi là hình nón nội tiếp mặt cầu
. Gọi
là chiều cao của hình nón đó.
a) Tính thể tích của hình nón theo và
.
b) Xác định để thể tích của hình nón là lớn nhất.
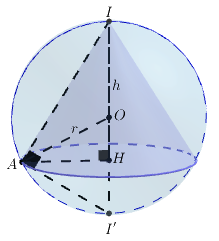
a)
+) Gọi là tâm của đường tròn
,
.
đối xứng với
qua
. Khi đó :
+) đồng dạng
b)
Ta có :
Vậy khi
Được tài trợ