Bài 5 trang 105 SGK Hình học 11
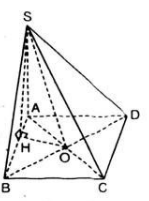
Trên mặt phẳng (α) cho hình bình hành ABCD tâm O. Gọi S là một điểm nằm ngoài mặt phẳng (α) sao cho SA = SC, SB = SD. Chứng minh rằng:
a) SO ⊥(α)
b) Nếu trong mặt phẳng (SAB) kẻ SH vuông góc với AB tại H thì AB vuông góc với mặt phẳng (SOH).
a) SA=SC⇒SAC cân tại S.
O là trung điểm của AC⇒SO là đường trung tuyến đồng thời là đường cao của tam giác cân nên SO⊥AC
Chứng minh tương tự ta có: SO⊥BD
Ta có:
.
b)
SO⊥(ABCD)⇒SO⊥AB (1)
Mà SH⊥AB (2)
Từ (1) và (2) suy ra AB⊥(SOH).
Được tài trợ