Bài 4 trang 105 SGK Hình học 11
Cho tứ diện OABC có ba cạnh OA,OB,OC đôi một vuông góc. Gọi H là chân đường vuông góc hạ từ O tới mặt phẳng (ABC). Chứng minh rằng:
a) H là trực tâm của tam giác ABC;
b) .
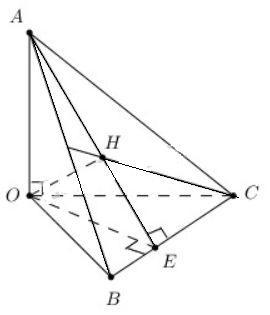
a) H là hình chiếu của O trên mp (ABC) nên OH⊥(ABC)⇒OH⊥BC. (1)
Mặt khác: OA⊥OB, OA⊥OC
⇒OA⊥(OBC)⇒OA⊥BC (2)
Từ (1) và (2) suy ra BC⊥(AOH)⇒BC⊥AH. Chứng minh tương tự ta được AB⊥CH
⇒H là trực tâm của tam giác ABC.
b) Trong mặt phẳng (ABC) gọi E=AH∩BC, OH⊥(ABC), AE⊂(ABC)⇒OH⊥AE tại H; tức là OH là đường cao của tam giác vuông OAE.
BC⊥(OAH)⇒BC⊥OE⇒OE là đường cao của tam giác vuông OBC.
Do đó:.
Được tài trợ