Bài 7 trang 105 SGK Hình học 11
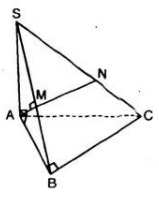
Cho tứ diện SABC có SA vuông góc với mặt phẳng (ABC) và tam giác ABC vuông tại B. Trong mặt phẳng (SAB), kẻ AM vuông góc với SB tại M. Trên cạnh SC lấy điểm N sao cho .
Chứng minh rằng:
a) BC ⊥ (SAB), AM ⊥ (SBC)
b) SB ⊥ AN.
a) SA⊥(ABC)⇒SA⊥BC (1),
Tam giác ABC vuông tại B nên BC⊥AB (2)
Từ (1) và (2) suy ra BC⊥(SAB).
BC⊥(SAB) nên BC⊥AM (3)
AM⊥SB (giả thiết) (4)
Từ (3) và (4) suy ra AM⊥(SBC).
b) AM⊥(SBC) nên AM⊥SB (5)
Giả thiết nên theo định lí ta lét ta có: MN//BC
Mà BC⊥SB (do BC⊥(SAB)) do đó MN⊥SB (6)
Từ (5) và (6) suy ra SB⊥(AMN) suy ra SB⊥AN.
Được tài trợ