Bài 5 trang 114 SGK Hình học 11
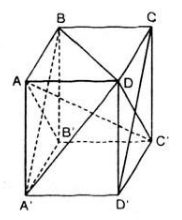
Bài 5 : Cho hình lập phương ABCD.A'B'C'D'. Chứng minh rằng:
a) Mặt phẳng (AB'C'D) vuông góc với (BCD'A')
b) Đường thẳng AC' vuông góc với mặt phẳng (A'BD).
a) BC⊥(ABB′A′)⇒BC⊥AB′;
Mà BA′⊥AB′⇒AB′⊥(BCD′A′).
Ta có AB′⊂(AB′C′D)⇒(AB′C′D)⊥(BCD′A′).
b)
AA′⊥(ABCD)⇒AA′⊥BD
Mà BD⊥AC⇒BD⊥(ACC′A′)
AC′⊂(ACC′A′) nên suy ra BD⊥AC′ (1)
AB⊥(ADD′A′)⇒AB⊥A′D
Mà AD′⊥A′D⇒A′D⊥(ABC′D′)
Ta có AC′⊂(ABC′D′)⇒A′D⊥AC′ (2)
Từ (1) và (2) suy ra: AC′⊥(A′BD).
Được tài trợ