Bài 11 trang 114 SGK Hình học 11
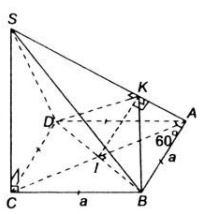
Cho hình chóp S.ABCD có đáy ABCD là một hình thoi tâm II cạnh aa và có góc A bằng 600, cạnh và SC vuông góc với mặt phẳng (ABCD).
a) Chứng minh mặt phẳng (SBD) vuông góc với mặt phẳng (SAC).
b) Trong tam giác SCA kẻ IK vuông góc với SA tại K. Hãy tính độ dài IK
c) Chứng minh và từ đó suy ra mặt phẳng (SAB) vuông góc với mặt phẳng (SAD).
a) SC⊥(ABCD)⇒SC⊥BD(1)
ABCD là hình thoi nên AC⊥BD(2)
Từ (1) và (2) suy ra BD⊥(SAC).
Mà BD⊂(SBD)⇒(SBD)⊥(SAC).
b) Xét tam giác vuông ABI có:
Xét tam giác vuông SAC có: .
Dễ dàng chứng minh đươc ΔSCA∼ΔIKA(g.g)
.
c) Dễ thấy ΔABD đều nên nên ΔBKD vuông tại K. Vậy
.
Ta có: BD⊥(SAC)(cmt)⇒BD⊥SA
Ta có:
⇒
⇒(SAB)⊥(SAD)
Được tài trợ