Bài 4 trang 114 SGK Hình học 11
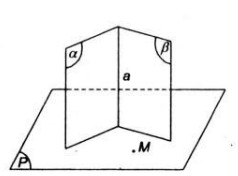
Bài 4: Cho hai mặt phẳng (α), (β) cắt nhau và một điểm M không thuộc (α) và (β). Chứng minh rằng qua điểm M có một và chỉ một mặt phẳng (P) vuông góc với (α) và (β). Nếu (α) // (β) thì kết quả trên sẽ thay đổi như thế nào?
Gọi a là giao tuyến của hai mặt phẳng (α) và (β).
Ta có:
Do đó mặt phẳng (P) đi qua M và vuông góc với đường thẳng a, do đó mặt phẳng (P) là duy nhất.
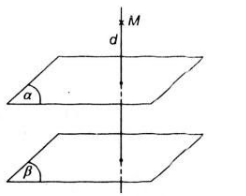
Nếu (α)//(β) gọi d là đường thẳng đi qua M và vuông góc với (α) khi đó ta có d⊥(β).
Như vậy mọi mặt phẳng chứa dd đều vuông góc với (α) và (β).
Do đó khi (α)//(β) thì có vô số mặt phẳng (P) đi qua M và vuông góc với (α)(α) và (β).
Được tài trợ