Bài 6 trang 114 SGK Hình học 11
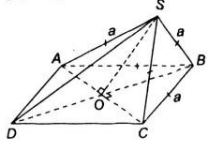
Bài 6: Cho hình chóp S.ABCD có đáy ABCD là một hình thoi cạnh a và có SA = SB = SC = a. Chứng minh rằng:
a) Mặt phẳng (ABCD) vuông góc với mặt phẳng (SBD).
b) Tam giác SBD là tam giác vuông.
a) Gọi O là giao điểm của hai đường chéo AC và BD
Theo tính chất của hình thoi thì O là trung điểm của AC,BD
Xét tam giác cân SAC cân tại S có SO vừa là đường trung tuyến đồng thời là đường cao do đó SO⊥AC (1)
Mặt khác ABCD là hình thoi nên AC⊥BD (2)
Từ (1) và (2) suy ra AC⊥(SBD)
AC⊂(ABCD)⇒(ABCD)⊥(SBD)
b) ΔSAC=ΔBAC(c.c.c)
Do đó các đường trung tuyến ứng với các đỉnh tương ứng của hai tam giác bằng nhau: SO=BO
O là trung điểm của BD nên OB=OD
Suy ra SO=OB=OD=BD
Đường trung tuyến ứng với một cạnh của tam giác và bằng nửa cạnh ấy thì tam giác đó là tam giác vuông. Do đó tam giác SBD vuông tại S