Bài 5 trang 50 SGK Hình học 12
Cho tứ diện đều cạnh
Gọi
là hình chiếu vuông góc của đỉnh
xuống mặt phẳng
.
a) Chứng minh là tâm đường tròn ngoại tiếp tam giác
. Tính độ dài đoạn
b) Tính diện tích xung quanh và thể tích của khối trụ có đường tròn đáy ngoại tiếp tam giác và chiều cao
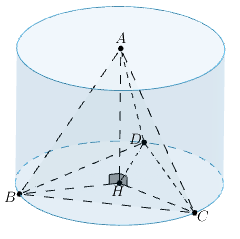
a)
+) Ta có
Tương tự ta có :
Vậy nên
là tâm đường tròn ngoại tiếp tam giác
+) đều cạnh
nên
cũng là trọng tâm tam giác
. Do đó :
b)
Khối trụ sinh ra có bán kính đáy đường sinh và chiều cao có độ dài là
Được tài trợ