Bài 6 trang 50 SGK Hình học 12
Cho hình vuông cạnh
. Từ tâm
của hình vuông dựng đường thẳng
vuông góc với mặt phẳng
. Trên
lấy điểm
sao cho
. Xác định tâm và bán kính mặt cầu ngoại tiếp hình chóp
Tính diện tích của mặt cầu và thể tích của khối cầu được tạo nên bởi mặt cầu đó.
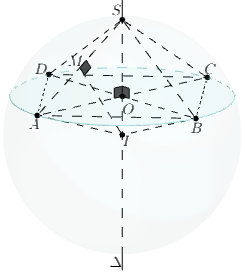
+) Vì là hình vuông tâm
và
nên
chính là trục của hình vuông. Do đó tâm mặt cầu ngoại tiếp của hình chóp thuộc vào
+) Trong mặt phẳng dựng đường trung trực của
cắt
tại
, ta có
nên
là tâm mặt cầu ngoại tiếp khối chóp, bán kính mặt cầu
Vì nằm giữa
. Khi đó
Vậy
Được tài trợ