I. Định nghĩa phương trình bậc bốn.

Là phương trình có dạng 

II. Cách giải một số phương trình bậc bốn đặc biệt.

1. Cách giải phương trình bậc bốn cơ bản : Dạng 

* Cách giải :

• Nếu  thì phương trình  vô nghiệm.
• Nếu  thì phương trình  trở thành 
• Nếu  thì phương trình 

Ví dụ 1. Giải phương trình                             

Ta có 

Ví dụ 2. Giải phương trình 

Ta có 

2. Cách giải phương trình bậc bốn trùng phương : 

* Nhận dạng : Là phương trình bậc bốn chỉ chứa  trong phương trình.

* Cách giải : Chú ý rằng  nên để giải phương trình này ta chỉ cần đặt  để đưa về phương trình bậc hai quen thuộc , từ đó tìm  và suy ra .

* Chú ý : Khi giải phương trình này ta thường gặp phương trình dạng . Khi đó cần lưu ý : 

• Nếu  thì phương trình 
• Nếu  thì phương trình 
• Nếu  thì phương trình  vô nghiệm (vì vế trái không âm mà vế phải là số âm).

* Ví dụ minh họa : 

Ví dụ 1. Giải phương trình : .

Lời giải :

Đặt , phương trình trở thành 

• Với  ta có 
• Với  ta có 

Vậy phương trình có tập nghiệm 

Ví dụ 2. Giải phương trình : .

Lời giải :

Đặt , phương trình trở thành 

• Với  ta có 
• Với  ta có  (vô nghiệm)

Vậy phương trình có nghiệm : 

Chú ý : Đối với hai ví dụ trên ta có thể xem chúng là các phương trình bậc hai đối với  nên ta có thể giải quyết nhanh gọn như sau 

• .

Ví dụ 3. Giải phương trình .

Phân tích : Rõ ràng vĩ dụ này chưa có dạng phương trình trùng phương nhưng cần lưu ý rằng . Như vậy ta có thể chuyển phương trình đã cho về một phương trình trùng phương theo . Từ đó có thể giải tương tự như trên.

Lời giải : 

Ta có 

Đặt  ta có phương trình : .

• Với  ta có 
• Với  ta có (vô nghiệm)

Vậy phương trình có nghiệm 

3. Cách giải phương trình bậc bốn có hệ số đối xứng : Dạng 

* Nhận dạng : Là một phương trình bậc bốn có hệ số đối xứng qua số hạng có 

* Cách giải :

• Bước 1 : Xét xem  có phải là nghiệm hay không bằng cách thay trực tiếp vào phương trình. Nếu không thỏa mãn thì không phải là nghiệm.
• Bước 2 : Với , do tính chất đối xứng ta thực hiện chia hai vế phương trình cho  đưa phương trình về dạng 
• Bước 3 : Đặt  và đưa  về theo . Từ đó giải phương trình theo t.

* Chú ý : Ta luôn có 

* Ví dụ minh họa : 

Ví dụ 1. Giải phương trình 

Phân tích : Rõ ràng các hệ số của phương trình đối xứng nhau qua số hạng có  nên ta giải theo phương pháp như trên.

Lời giải : 

+ Trường hợp 1 : Với  phương trình trở thành  (vô lí). Vậy  không phải là nghiệm của phương trình.

+ Trường hợp 2 : Với , chia hai vế của phương trình cho  ta có phương trình 

Đặt   phương trình trở thành : 

• Với  ta có 
• Với  ta có 

Vậy phương trình có tập nghiệm 

Ví dụ 2. Giải phương trình 

Lời giải :

+ Trường hợp 1 : Với  không thỏa mãn phương trình đã cho.

+ Trường hợp 2 : Với , chia hai vế phương trình cho  ta được phương trình 

+ Đặt , phương trình trở thành 

• Với  ta có 
• Với  ta có 

+ Vậy phương trình có nghiệm 

Lưu ý : Việc xét hai trường hợp như trên là cần thiết vì muốn chia hai vế phương trình cho một số thì số đó phải khác 0.

4. Cách giải phương trình bậc bốn khi đã nhẩm trước ít nhất hai nghiệm.

Khi gặp một phương trình bậc bốn không thuộc các dạng đặc biệt như trên thì ta có thể nhẩm trước hai nghiệm và tìm cách đưa phương trình đã cho về dạng phương trình tích. Phương pháp này chỉ áp dụng khi ta đã biết trước hai nghiệm (thường là nghiệm nguyên) của phương trình đó.Cách làm như sau : 

Xét phương trình dạng 

Bước 1. Từ phương trình đã cho tính nhẩm hai nghiệm (có thể dùng máy tính hỗ trợ).

Bước 2. Thực hiện phép chia  cho  (lưu ý rằng đây là phép chia hết).

Bước 3. Đưa phương trình đã cho về dạng  Giải phương trình tích này tìm 

* Lưu ý : Các bước 1, 2 ta có thể thực hiện trên giấy nháp để lấy kết quả sử dụng cho bước 3.

Ví dụ 1: Giải phương trình .

+ Nhận thấy rằng phương trình có nghiệm .

+ Thực hiện phép chia  cho  như sau:
 

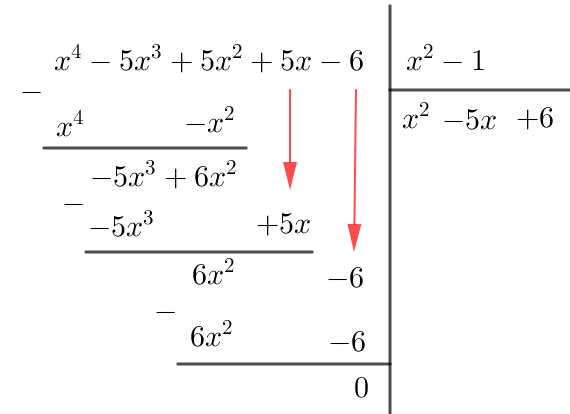
+ Từ đây ta có : . 

+ Như vậy ta sẽ đưa phương trình đã cho về dạng tích  Vì vậy ta có lời giải bài này như sau 

Lời giải : 

Ta có : undefined

Vậy phương trình có tập nghiệm 

Ví dụ 2 : Giải phương trình 

+ Nhận thấy phương trình có nghiệm .

Thực hiện phép chia  cho  như sau
 

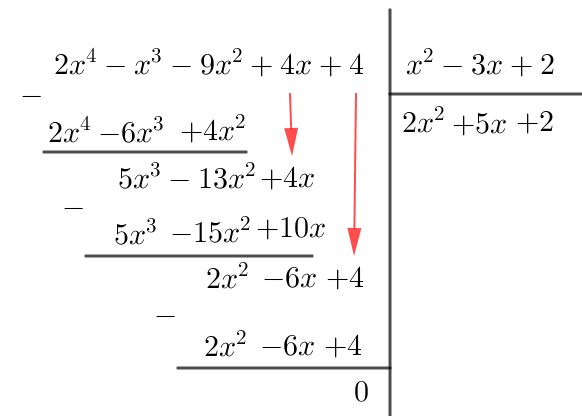
Vậy ta có 

Lời giải :

Ta có .

Vậy phương trình có nghiệm 

Chú ý : Cách làm này có thể áp dụng để giải phương trình bậc ba và đối với phương trình bậc ba ta chỉ cần nhẩm được một nghiệm  rồi thực hiện phép chia cho 

5. Cách giải phương trình bậc bốn bằng phương pháp đồng nhất hệ số.

Đây là phương pháp đặc biệt được áp dụng khi giải phương trình bậc 4 không có nghiệm nguyên và chỉ giải quyết được một số bài toán nhất định bằng cách phân tích một đa thức bậc bốn thành tích của hai tam thức bậc hai với giả định : . Bài toán có giải quyết được hay không phụ thuộc vào việc có tìm được các hệ số  hay không.

Ví dụ 1 : Giải phương trình 

+ Nhận xét rằng, trong ví dụ ta sẽ khó nhẩm được nghiệm, do đó ta nghĩ đến phương án cân bằng hệ số như sau : Giả sử 

+ Ta sẽ đi tìm các số  thỏa mãn (*). 

Đồng nhất các hệ số ta có . Do  nên ta chọn  , khi đó hệ trở thành . Giải hệ này bằng phương pháp thế ta có 

+ Thay các giá trị tìm được vào (*) ta có  . Tới đây ta có thể giải quyêt dễ dàng bài toán.

+ Lưu ý rằng việc đồng nhất hệ số được thực hiện trên giấy nháp.

Lời giải : 

Ta có .

Ví dụ 2 : Giải phương trình 

+ Giả sử 

+ Đồng nhất các hệ số ta có . Vì  ta có thể chọn , khi đó hệ trở thành . Giải hệ này tìm được .

+ Vậy ta có : 

Lời giải : 

Ta có