Bài 10 trang 81 SGK Hình học 12
Giải bài toán sau bằng phương pháp tọa độ: Cho hình lập phương cạnh bằng 1.
a) Chứng minh rằng hai mặt phẳng và
song song với nhau.
b) Tính khoảng cách giữa hai mặt phẳng nói trên.
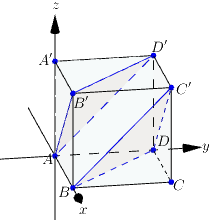
Chọn hệ trục tọa độ như hình vẽ với : gốc tọa độ là
Khi đó : và
a)
Mp đi qua
và chứa hai vec tơ
nên có vec tơ pháp tuyến :
Phương trình mặt phẳng
Mpchứa hai vec tơ
nên có vec tơ pháp tuyến :
.
Rõ ràng nên chúng cùng phương và
Vậy
b)
Vì nên
Được tài trợ