Bài 10 trang 91 SGK Hình học 12
Giải bài toán sau bằng phương pháp tọa độ: Cho hình lập phương có cạnh bằng 1. Tính khoảng cách từ đỉnh
đến các mặt phẳng
và
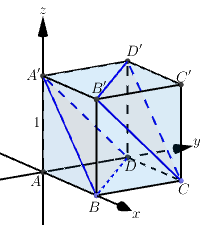
Chọn hệ trục tọa độ như hình vẽ, khi đó : và
+) Mpđi qua
có vec tơ pháp tuyến
nên có phương trình
+) Mp nên nhận
làm vec tơ pháp tuyến đồng thời đi qua C nên có phương trình :
Được tài trợ