Bài 1 trang 145 SGK Giải tích 12
Cho hàm số
a) Chứng tỏ rằng phương trình luôn có nghiệm thực. Tính các nghiệm đó.
b) Tính tổng và tích
của các nghiệm của phương trình
Khảo sát sự biến thiên và vẽ đồ thị của
và
theo
.
a) Xét phương trình : khi đó :
- Với
ta có :
nên phương trình có hai nghiệm phân biệt
- Vậy phương trình luôn có nghiệm
hoặc
b) Theo định lí Vi-ét ta có :
*) Khảo sát và vẽ đồ thị của
+) Tập xác định :
+) Sự biến thiên:
-
Hàm số nghịch biến trên từng khoảng xác định.
- Các giới hạn :
là tiệm cận ngang.
là tiệm cận đứng.
- Bảng biến thiên :
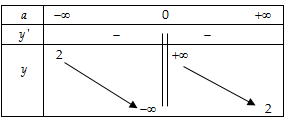
- Hàm số không có cực trị.
+) Đồ thị : Điểm đặc biệt
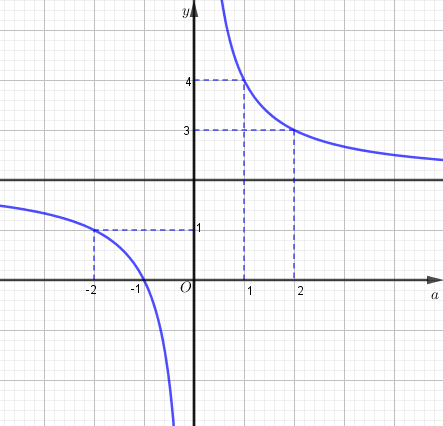
*) Khảo sát và vẽ : Đặt
ta có
+) Tập xác định :
+) Sự biến thiên :
Vậy hàm số nghịch biến trên từng khoảng xác định.
- Các giới hạn :
là tiệm cận ngang và
là tiệm cận đứng.
- Bảng biến thiên :
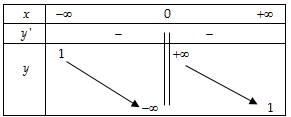
- Hàm số không có cực trị.
+) Đồ thị : Điểm đặc biệt
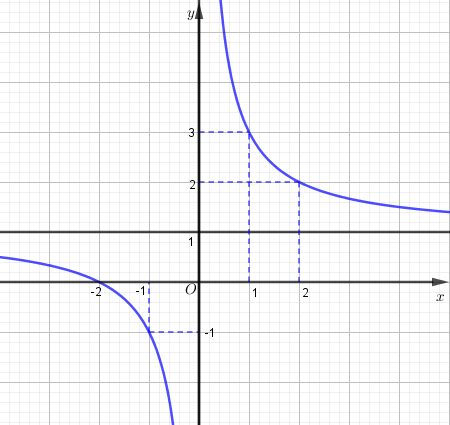
Được tài trợ