Bài 8 trang 40 SGK Hình học 12
Một hình trụ có hai đáy là hai hình tròn và
. Khoảng cách giữa hai đáy là
Một hình nón có đỉnh là
và có đáy là hình tròn
a) Gọi là diện tích xung quanh hình trụ và
là diện tích xung quanh của hình nón, hãy tính tỉ số
b) Mặt xung quanh của hình nón chia khối trụ thành hai phần, hãy tính tỉ số thể tích hai phần đó.
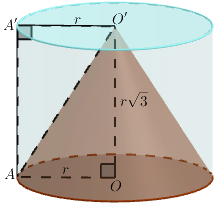
a) Gọi , kẻ đường thẳng qua
song song
. Đường thẳng này cắt
tại
Ta có :
Vậy
b)
+) Mặt xung quanh của hình nón chia khối trụ thành hai phần. Phần là thể tích khối nón. Phần
là phần giới hạn bởi khối trụ và khối nón.
+) Gọi là thể tích khối trụ ta có :
+) Thể tích khối nón :
+) Vậy
Được tài trợ