Bài 7 trang 39+40 SGK Hình học 12
Một hình trụ có bán kính 
và chiều cao 
a) Tính diện tích xung quanh và diện tích toàn phần của hình trụ.
b) Tính thể tích khối trụ sinh ra bởi hình trụ đã cho.
c) Cho hai điểm 
và 
lần lượt nằm trên hai đường tròn đáy sao cho góc giữa đường thẳng 
và trục của hình trụ bằng 
Tính khoảng cách giữa đường thẳng và trục của hình trụ.
a) Ta có : 
b) 
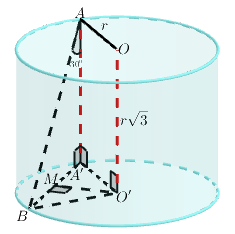
c) Gọi 
lần lượt là tâm của hai đáy của hình trụ. 
lần lượt thuộc đường tròn tâm 
.
+) Từ điểm kẻ đường thẳng song song với trục hình trụ. Rõ ràng đường thẳng này nằm trong mặt trụ nên cắt đường tròn tâm 
tại một điểm. Kí hiệu là 
+) Ta có 
+) Mặt khác : 
- Gọi
![]()
là trung điểm ![]()
![]()
![]()
vuông tại ![]()
![]()
là trung điểm 
vuông tại 
+) Vậy 
Được tài trợ