Bài 9 trang 40 SGK Hình học 12
Cắt hình nón đỉnh bởi mặt phẳng đi qua trục ta được một tam giác vuông cân có cạnh huyền bằng
.
a) Tính diện tích xung quanh, diện tích đáy và thể tích của khối nón tương ứng.
b) Cho dây cung của đường tròn đáy hình nón sao cho mặt phẳng
tạo với mặt phẳng chứa đáy hình nón một góc
. Tính diện tích tam giác
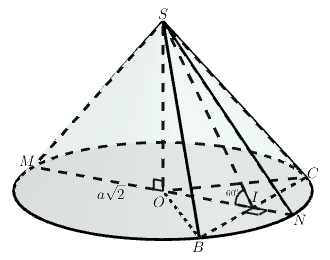
a)
+) Tam giác vuông cân tại
b)
+) Các tam giác lần lượt cân tại
và
. Gọi
là trung điểm
ta có
+) Tam giác vuông tại
và
+) Vậy
Được tài trợ