Câu 4 Trang 93 SGK Hình học 10
Cho đường thẳng Δ:x–y+2 và hai điểm O(0;0);A(2;0)
a) Tìm điểm đối xứng của O qua Δ
b) Tìm điểm M trên Δ sao cho độ dài đường gấp khúc OMA ngắn nhất.
a) Gọi H là hình chiếu của O trên Δ,H là giao điểm của đường thẳng qua O và vuông góc với Δ.
Δ:x–y+2=0 có vecto chỉ phương
Tọa độ điểm H là nghiệm của hệ phương trình:
Gọi O′ là đỉnh đối xứng của O qua Δ thì H là trung điểm của đoạn thẳng OO′
Vậy O′(−2;2).
b) Nối O′A cắt Δ tại M
Ta có: OM=O′M
⇒OM+MA=O′M+MA=O′A
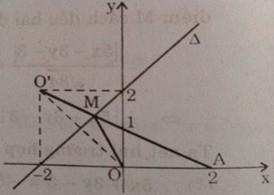
Giả sử trên Δ có một điểm M′≠M, ta có ngay:
OM′+M′A>O′A
Vậy điểm M, giao điểm của O′A với Δ, chính là điểm thuộc Δ mà độ dài của đường gấp khúc OMA ngắn nhất.
A(2;0);O(−2;2) nên O′A có hệ phương trình: x+2y–2=0
Tọa độ của điểm M là nghiệm của hệ:
.
Được tài trợ