Bài 5 trang 44 SGK Giải tích 12

a) 

+) Tập xác định: 

+) Sự biến thiên:

• Đạo hàm: 
• Giới hạn vô cực: 
• Bảng biến thiên:

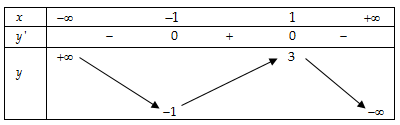
• Tính đơn điệu: Hàm số đồng biến trên ; nghịch biến trên các khoảng 
• Cực trị: Hàm số đạt cực đại tại , đạt cực tiểu tại 

+) Đồ thị:

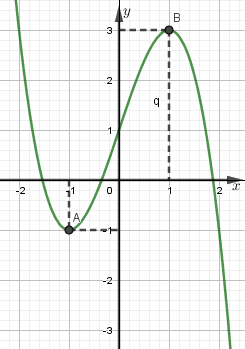
b) Xét phương trình: 

+) Ta có số nghiệm của phương trình đã cho chính là số giao điểm của đồ thị hai hàm số .

+) Dựa vào đồ thị  ta thấy: 

• Nếu  thì phương trình có một nghiệm duy nhất.
• Nếu  thì phương trình có hai nghiệm phân biệt.
• Nếu  thì phương trình đã cho có ba nghiệm phân biệt.