Bài 6 trang 44 SGK Giải tích 12

a) 

•  Tập xác định: 
• . Vậy hàm số luôn đồng biến trên mỗi khoảng xác định của nó.

b) Xét  ta có:

• Do đó  là tiệm cận đứng của đồ thị hàm số.
• Để tiệm cận đứng đi qua  ta có .

c) Khảo sát và vẽ khi : Với  ta có 

+)Tập xác định: 

+) Sự biến thiên:

•  
•  là tiệm cận đứng
•  là tiệm cận ngang.
• Bảng biến thiên: 

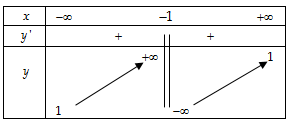
• Hàm số đồng biến trên các khoảng 
• Hàm số không có cực trị.

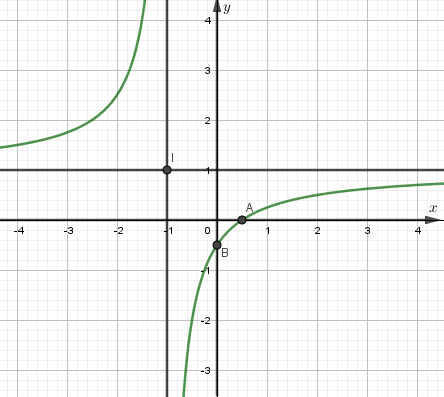
+) Đồ thị: Điểm đặc biệt