Bài 9 trang 49 SGK Hình học 12
Cho một điểm cố định và một đường thẳng
cố định không đi qua
.Gọi
là một điểm thay đổi trên
. Chứng minh rằng các mặt cầu tâm
bán kính
luôn luôn đi qua một đường tròn cố định.
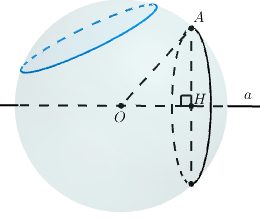
+) Theo giả thiết ta có điểm và đường thẳng
cố định. Dựng mặt phẳng
chứa
và vuông góc với
. Khi đó mp
cũng cố định. Gọi
+) Xét mặt cầu tâm bán kính
, mặt cầu này cắt mặt phẳng
theo giao tuyến là đường tròn tâm
bán kính
không đổi.
+) Vậy các mặt cầu tâm bán kính
luôn đi qua đường tròn tâm
bán kính
không đổi.
Được tài trợ