Bài 10 trang 27 SGK Hình học 12
Cho hình lăng trụ đứng tam giác có tất cả các cạnh đều bằng
.
a) Tính thể tích khối tứ diện
b) Mặt phẳng đi qua và trọng tâm tam giác
cắt
và
lần lượt tại
và
Tính thể tích hình chóp
a) Tam giác đều cạnh
, gọi
là trung điểm của
ta có :
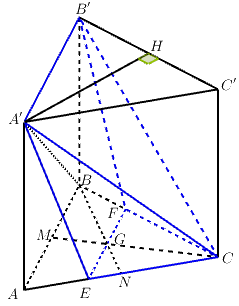
b) Gọi là trọng tâm tam giác
. Vì
nên mặt phẳng chứa
qua
cắt
theo giao tuyến đi qua
và song song
Giao tuyến này cắt
lần lượt tại
+) Ta có :
+) Mặt khác : là trọng tâm tam giác
nên
,
+) Vậy
Được tài trợ