Bài 11 trang 27 SGK Hình học 12
Cho hình hộp Gọi
và
theo thứ tự là trung điểm các cạnh
và
. Mặt phẳng
chia khối hộp trên làm hai khối đa diện. Tính tỉ số thể tích của hai khối đa diện đó.
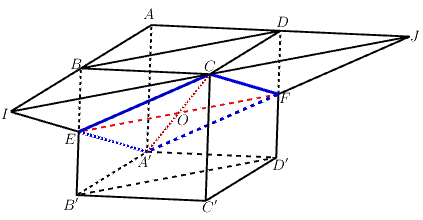
+) Ta có nên mp
cắt
theo giao tuyến đi qua
và song song
. Giao tuyến này cắt
lần lượt tại
+) Ta chứng minh : thẳng hàng
- Thật vậy : Giả sử
không thẳng hàng, khi đó
(mâu thuẩn).
+) Tương tự ta có : thẳng hàng.
+) lần lượt là trung điểm của
là hình bình hành.
+) Vậy thiết diện tạo bới là hình bình hành
+) Gọi lần lượt là thể tích của khối đa diện
+) Khi đó : ,
- Tương tự :
Vậy
Được tài trợ