Bài 12 trang 27 SGK Hình học 12
Cho hình lập phương 
cạnh 
. Gọi 
là trung điểm 
, 
là trung điểm 
a) Tính thể tích khối tứ diện 
b) Mặt phẳng 
chia khối lập phương đã cho thành hai khối đa diện. Gọi 
là khối đa diện chứa đỉnh 
là khối đa diện còn lại. Tính tỉ số 
a) Nhận xét rằng : 
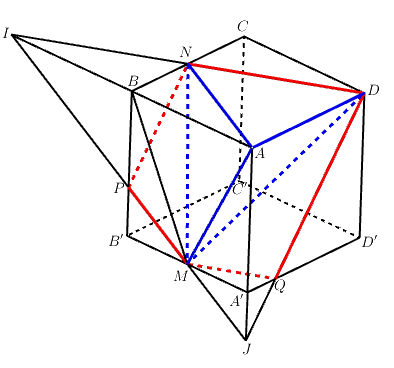
b)
+) Trong 
+) Trong 
+) Trong 
Thiết diện tạo bởi là ngũ giác 
+) Khi đó : 
- Ta có
![]()
nên ![]()
đồng dạng ![]()
![]()
- Lại có
![]()
nên ![]()
và ![]()
đồng dạng ![]()
nên 
đồng dạng 
nên 
và 
đồng dạng 
+) Vậy 
Được tài trợ