Bài 8 trang 26 SGK Hình học 12
Cho hình chóp 
có đáy 
là hình chữ nhật, 
vuông góc với đáy và 
Lấy các điểm 
theo thứ tự thuộc 
sao cho 
vuông góc 
, 
vuông góc với 
. Mặt phẳng 
cắt 
tại 
Tính thể tích khối chóp 
+) Trong 
trong 
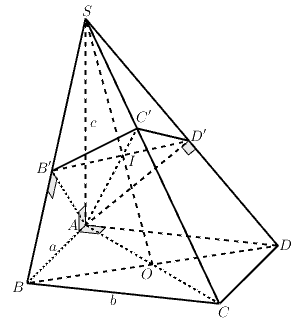
+) Trong 
gọi 
+) Ta có : 
+) 
+) Mặt khác :
- Tam giác
![]()
vuông tại ![]()
là đường cao nên :![]()
- Tương tự ta có :
![]()
vuông tại 
là đường cao nên :
+) Theo giả thiết ta có : 
+) Tương tự ta có : 
- Tam giác
![]()
vuông tại ![]()
là đường cao nên : ![]()
vuông tại 
là đường cao nên : 
+) Vậy 
Được tài trợ