Bài 7 trang 26 SGK Hình học 12
Cho hình chóp 
có 
Các mặt bên 
tạo với đáy một góc 
Tính thể tích khối chóp đó.
+) Gọi 
là hình chiếu của 
lên mặt phẳng 
. Từ kẻ 
lần lượt vuông góc với 
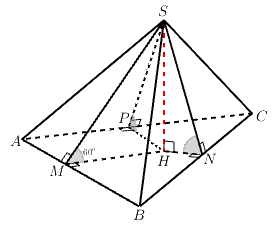
+) Ta có :
![]()
tương tự ta có: ![]()
![]()
Vậy ![]()
là tâm đường tròn nội tiếp ![]()
.
tương tự ta có: 
Vậy 
.+) Mặt khác : 
+) Vậy 
Được tài trợ