Bài 9 trang 26 SGK Hình học 12
Cho hình chóp đều đáy là hình vuông cạnh
, cạnh bên tạo với đáy một góc
Gọi
là trung điểm
. Mặt phẳng đi qua
và song song
, cắt
tại
và cắt
tại
. Tính thể tích khối chóp
+) Trong trong
:
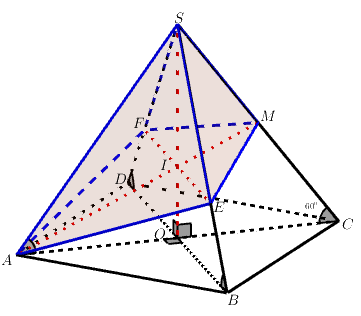
+) Mặt phẳng chứa và song song
nên cắt
theo giao tuyến đi qua
và song song
Giao tuyến này cắt
lần lượt tại
+) là hình chóp đều nên
+) Theo giả thiết ta có : Do đó
đều cạnh bằng
+) Mặt khác là trọng tâm tam giác
và
+) Vậy
Được tài trợ