Bài 6 trang 45 SGK Giải tích 12
a) Khảo sát sự biến thiên và vẽ đồ thị 
của hàm số 
b) Giải bất phương trình 
c) Viết phương trình tiếp tuyến của đồ thị tại điểm có hoành độ 
, biết rằng 
a) 
+) Tập xác định: 
+) Sự biến thiên:
- Đạo hàm:
![]()
. - Giới hạn:
![]()
- Bảng biến thiên:
.
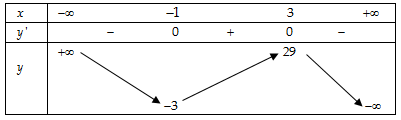
- Vậy hàm số đồng biến trên khoảng
![]()
và nghịch biến trên các khoảng ![]()
- Hàm số đạt cực tiểu tại
![]()
; đạt cực đại tại ![]()
và nghịch biến trên các khoảng 
; đạt cực đại tại 
+) Đồ thị: Điểm đặc biệt 
b) Giải phương trình 
.
Ta có 
Khi đó 
Vậy bất phương trình đã cho có nghiệm 
c) Ta có 
.
Khi đó 
Vậy phương trình tiếp tuyến cần tìm là: 
Được tài trợ