Bài 11 trang 46 SGK Giải tích 12
a) Khảo sát sự biến thiên và vẽ đồ thị 
của hàm số 
b) Chứng minh rằng với mọi giá trị của 
, đường thẳng 
luôn cắt tại hai điểm phân biệt 
.
c) Xác định sao cho độ dài 
là nhỏ nhất.
d) Tiếp tuyến tại một điểm 
bất kì của cắt hai tiệm cận của 
tại 
và 
. Chứng minh là trung điểm 
a) 
+) Tập xác định: 
+) Sự biến thiên:
- Đạo hàm:
![]()
- Tiệm cận:
![]()
là tiệm cận đứng.
là tiệm cận đứng. 
là tiệm cận ngang.
- Bảng biến thiên:
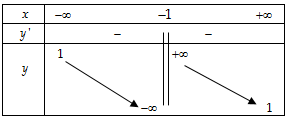
- Tính đơn điệu: Hàm số nghịch biến trên các khoảng
![]()
- Cực trị: Hàm số không có cực trị.
+) Đồ thị: Điểm đặc biệt 
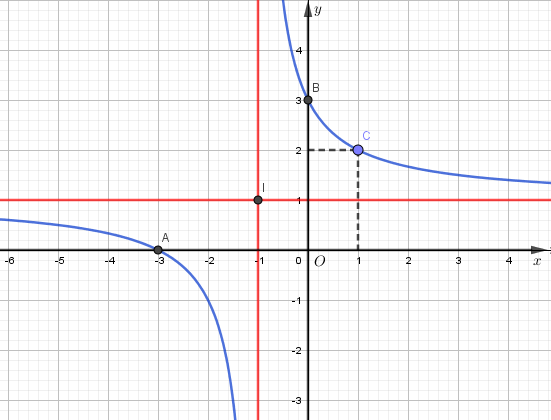
b) Xét phương trình hoành độ giao điểm: 
+) 
+) Mặt khác 
+) Từ 
và 
suy ra phương trình hoành độ giao điểm luôn có hai nghiệm phân biệt khác -1. Do đó đường thẳng luôn cắt tại hai điểm phân biệt 
.
c) Gọi 
. Khi đó:
+) 
. Dấu bằng đạt tại 
d) Gọi 
. Khi đó tiếp tuyến tại có dạng 
+) Tiệm cận đứng là 
; tiệm cận ngang 
.
+) Vậy ta có 
là trung điểm của 
Được tài trợ