Bài 7 trang 45+46 SGK Giải tích 12

a) 

+) Tập xác định: 

+) Sự biến thiên:

• Đạo hàm 
• Các giới hạn: 
• Bảng biến thiên:

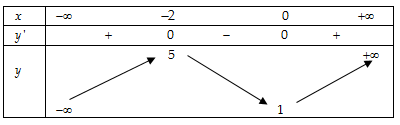
• Hàm số đồng biến trên các khoảng  và nghịch biến trên khoảng 
• Hàm số đạt cực đại tại , đạt cực tiểu tại 

+) Đồ thị: Điểm đặc biệt 

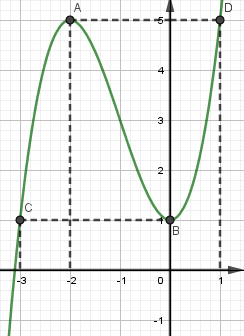
b) Xét phương trình 

Số nghiệm của phương trình  chính là số giao điểm của đồ thị hai hàm số . Dựa vào đồ thị  ta có:

• Nếu tức là  thì phương trình có duy nhất một nghiệm.
• Nếu  tức là  thì phương trình có hai nghiệm phân biệt.
• Tương tự nếu  thì phương trình có ba nghiệm phân biệt.

c) Điểm cực đại của hàm số là , điểm cực tiểu là . Khi đó .

Đường thẳng  đi qua  có vectơ pháp tuyến  có phương trình: