Bài 14 trang 101 SGK Hình học 12
Trong không gian cho ba điểm
a) Xác định điểm sao cho
b) Tìm tập hợp các điểm sao cho
với
là hằng số.
a) Ta chỉ xét trường hợp không thẳng hàng.
Xét biểu thức :
Gọi điểm sao cho
Khi đó ta có :
là đỉnh còn lại của hình bình hành
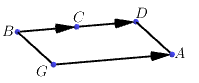
b)
Xét biểu thức : (vì
)
Vì vậy :
+) Nếu thì tập hợp điểm
là mặt cầu tâm
, bán kính
+) Nếu
+) Nếu thì tập hợp điểm
là tậm rỗng (không có M).
Được tài trợ