Bài 4 trang 99 SGK Hình học 12
Trong không gian , cho hai điểm
và đường thẳng d có phương trình
a) Chứng minh rằng hai đường thẳng và
cùng nằm trong một mặt phẳng.
b) Tìm điểm trên
sao cho
nhỏ nhất.
a)
+) Ta có : có vec tơ chỉ phương
và
. Suy ra
song song hoặc trùng nhau.
+) Mặt khác : không thỏa mãn phương trình của
nên
Vậy hay chúng cùng nằm trong một mặt phẳng.
b)
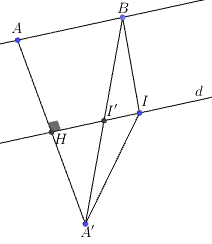
+) Do nên
nằm về cùng một phía so với
. Gọi
là điểm đối xứng của
qua
. Khi đó
. Vậy
, dấu bằng xãy ra khi
+) Gọi là mặt phẳng qua
và vuông góc với
, khi đó
có phương trình :
+) nên tọa độ
là nghiệm của hệ :
Do là trung điểm
nên
Suy ra có phương trình :
+) Vậy nên tọa độ điểm
cần tìm là nghiệm của hệ :
Được tài trợ