Bài 5 trang 99 SGK Hình học 12
Cho tứ diện có cạnh
vuông góc với mặt phẳng
. Biết rằng
a) Tính thể tích tứ diện
b) Tính khoảng cách từ điểm tới mặt phẳng
a) Ta có vuông tại
Vậy
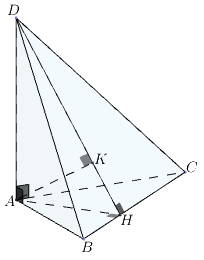
b) Gọi là chân đường cao kẻ từ
của tam giác
, ta có
+) Trong tam giác gọi
là chân đường cao kẻ từ
, khi đó
+) Tính
vuông tại
nên
Được tài trợ