Bài 6 trang 142 SGK Đại số và Giải tích 11
Bài 6. Cho hai hàm số và
a) Tính
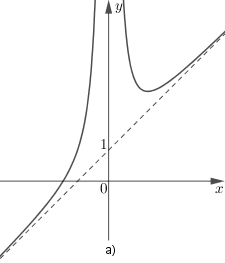
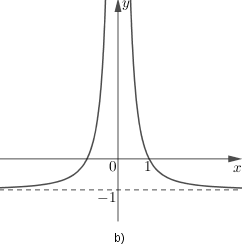
b) Hai đường cong sau đây (h.60) là đồ thị của hai hàm số đã cho. Từ kết quả câu a), hãy xác định xem đường cong nào là đồ thị của mỗi hàm số đó.
 |
 |
a)
b) Gọi lần lượt là hai đồ thị của hàm số
+ Vì nên hai đồ thị có nhánh đi lên vô tận khi
+) Vì nên
có nhánh vô tận tiến gần đến đường thẳng
khi
+) Vì nên
có nhánh vô tận đi lên khi
Dựa vào đặc điểm của như trên ta có
là đồ thị b) và
là đồ thị a).
Được tài trợ